Current Affairs Ebook Free PDF: Download Here
Attempt Free Mock Tests- Click Here
Table of content
Regular PolygonDefinition Regular of Polygon
Formula of Regular Polygon
Interior Angles in Regular Polygons
Sum of a Polygon's Interior Angles
Regular Polygon area
Shapes of Regular polygon
Regular Polygon
Regular polygons are those whose interior angles and all of their sides are equal. It is created using straight lines of the same length, and the straight line-created angles have the same size as well. Squares, rhombuses, equilateral triangles, and other shapes are examples of regular polygons.Definition Regular of Polygon
A closed figure with all of its sides and angles equal is referred to as a regular polygon. It is a closed two-dimensional figure that lies along a finite number of straight, equal-length lines. The lines come together at a place known as the vertex or corner, where they also form an angle. The accompanying figure shows the regular polygons.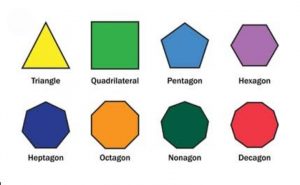
Formula of Regular Polygon
Regular polygons are two-dimensional closed figures with finite straight lines, as we have explained. It is composed of straight lines that connect together. Here is a list of the formulae used in a regular polygon.Sum of Interior Angles of a Regular Polygon Calculation Formula
For a regular ‘n’ sided polygon, the sum of interior angles of a polygon is 180°(n-2)
The equation for calculating a regular polygon's number of diagonals
The number of diagonals of an “n-sided” polygon = [n(n-3)]/2
How to calculate a regular polygon's interior angles using a formula
The measure of each interior angle of a regular n-sided polygon = [(n-2)180°]/n
The equation to calculate the exterior angle of a regular polygon
The measure of exterior angles of a regular n-sided polygon = 360°/n
The formula for finding the area of a regular polygon
Area of regular polygon = (number of sides × length of one side × apothem)/2, where, the length of apothem is given as the
A = l²n/4 tan(π/l)
Interior Angles in Regular Polygons
The two rays are joined at a single point to produce an angle, as is well known. Regular polygons have equal sides and angles, resulting in the formation of an equal number of angles and sides. The angle created by two adjacent sides inside the figure is known as an interior angle. With sides joining at a location in the figure, the interior angles are created. The inner angles are expressed as radians or degrees.Sum of a Polygon's Interior Angles
For various figures, a polygon's internal angle total varies. It can be simply calculated because it is a constant value. Here, it is described how to calculate a polygon's inner angle sum.Sum of the Interior Angles of a Polygon = 180 (n-2) degrees
Where n = number of sides of the polygon
| Polygon shapes | Number of Interior Angles | Sum of Interior Angles = (n-2) x 180° |
| Triangle | 3 | 180° |
| Quadrilateral | 4 | 360° |
| Pentagon | 5 | 540° |
| Hexagon | 6 | 720° |
| Septagon | 7 | 900° |
| Octagon | 8 | 1080° |
| Nonagon | 9 | 1260° |
| Decagon | 10 | 1440° |
Regular Polygon area
The sides and angles of a regular polygon are identical. A regular polygon's area is defined as the entire area contained within the closed figure. There are situations when an apothem is employed to calculate the area of a regular polygon. The line segment that connects the centre of the polygon to the midpoint of any side and is perpendicular to that side is referred to as an apothem. A regular polygon's vertices are all located on a circle that passes through it or on what is known as an inscribed circle that forms a tangent in the middle of each side. The term "tangential polygon" also refers to a regular polygon. The figure below depicts a regular polygon with n sides.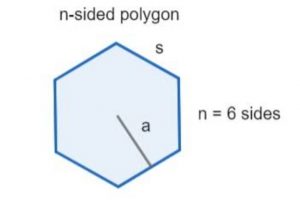
The formula to calculate the area of a regular polygon is shown here
A = l²n/4 tan(π/l)
Where l = length of the side of the polygon
and, n = number of sides
Shapes of Regular polygon
A regular polygon is a two-dimensional closed figure having all sides and angles equal. The regular polygon has infinite straight lines. The shapes of regular polygons are shown in the above figure. It has many shapes like triangle, square, rhombus, pentagon, hexagon, septagon, octagon, nonagon, decagon, etc.Also check,
What is a regular polygon?
The shapes with equal lines and angles are called regular polygons. It is a closed, two-dimensional figure constructed from finite straight lines.What is the second?
Apothem is the line segment that connects the midpoint of any side to the polygon's centre, and it is perpendicular to that side.
What is a regular polygon's area?
The region covered inside the figure is the area a on f regular polygon, which can be easily determined using the formula A = l2n/4 tan(/l).
